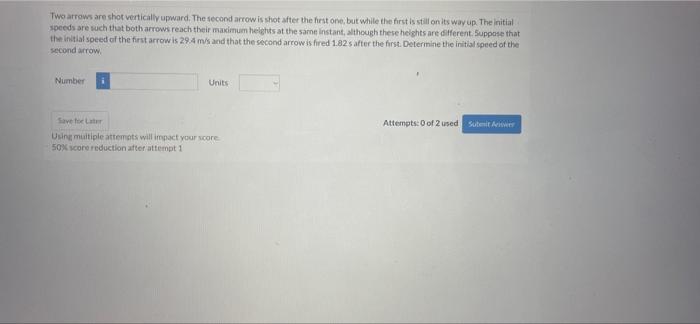
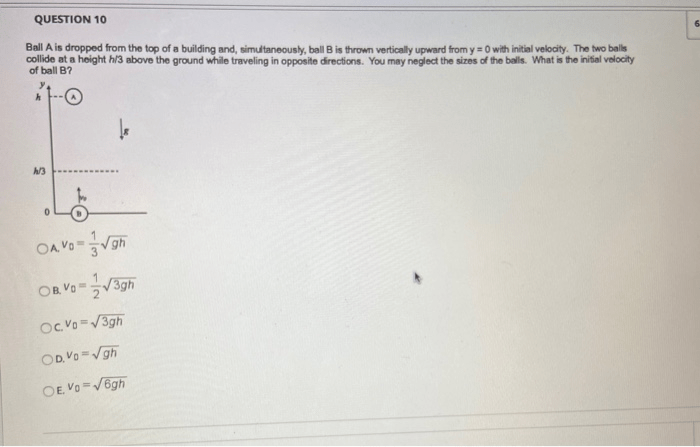
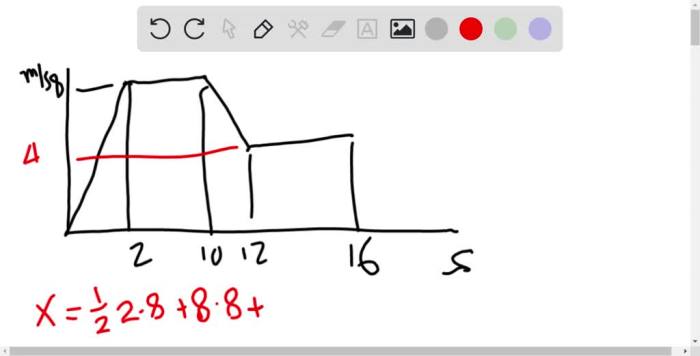
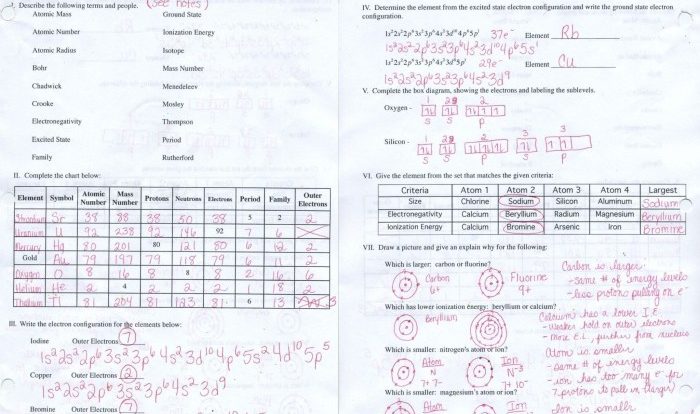
Two arrows are shot vertically upward, embarking on a journey that unravels the intricacies of projectile motion. This captivating narrative delves into the governing equations, initial conditions, and assumptions that shape the arrows’ trajectory, velocity, and acceleration. Prepare to witness the interplay of energy transformations, air resistance, and the interplay of graphical representations that illuminate the arrows’ remarkable ascent and descent.

Kinematics of Vertical Projectile Motion

Vertical projectile motion is the motion of an object thrown or projected vertically upward in a gravitational field. The object’s initial velocity is vertical and upward, and its acceleration is due to gravity, which is constant and downward. The governing equations for vertical projectile motion are:

• -*Velocity

  v = u + at

-*Displacement

s = ut + 1/2 at^2

-*Acceleration

a = g

where:

• v is the velocity at time t
• u is the initial velocity
• a is the acceleration due to gravity (g = 9.8 m/s^2 on Earth)
• t is the time
• s is the displacement

The initial conditions for vertical projectile motion are that the object is at the origin (s = 0) at time t = 0. The assumptions made are that the acceleration due to gravity is constant and that there is no air resistance.

Trajectory and Velocity, Two arrows are shot vertically upward

The trajectory of the arrows as they move vertically upward is a parabola. The velocity of the arrows is initially upward and decreases as they rise due to the acceleration due to gravity. At the maximum height, the velocity of the arrows is zero.

The arrows then fall back to the ground, and their velocity increases as they fall.

Maximum Height and Time of Flight

The maximum height reached by the arrows is given by the equation:“`h = u^2 / 2g“`where:

• h is the maximum height
• u is the initial velocity
• g is the acceleration due to gravity

The time it takes for the arrows to reach their maximum height is given by the equation:“`t = u / g“`where:

• t is the time to reach maximum height
• u is the initial velocity
• g is the acceleration due to gravity

The time it takes for the arrows to return to the ground is given by the equation:“`t = 2u / g“`where:

• t is the time to return to the ground
• u is the initial velocity
• g is the acceleration due to gravity

Effect of Initial Velocity

The initial velocity of the arrows affects their trajectory, maximum height, and time of flight. A higher initial velocity results in a higher maximum height and a longer time of flight.

Air Resistance and Drag

Air resistance and drag act on the arrows as they move through the air. These forces oppose the motion of the arrows and cause them to decelerate. The effects of air resistance and drag are more significant for objects with a large surface area or low mass.

Energy Considerations

The arrows have kinetic energy due to their motion and potential energy due to their height above the ground. The total energy of the arrows is conserved throughout their flight. At the maximum height, the arrows have zero kinetic energy and maximum potential energy.

As the arrows fall, their potential energy is converted into kinetic energy.

Graphical Representation

The trajectory, velocity, and acceleration of the arrows can be represented graphically. The trajectory is a parabola, the velocity is a straight line that decreases as the arrows rise and increases as they fall, and the acceleration is a constant downward line.

Question & Answer Hub: Two Arrows Are Shot Vertically Upward

What factors influence the maximum height reached by the arrows?

The maximum height is determined by the initial velocity and the acceleration due to gravity.

How does air resistance affect the motion of the arrows?

Air resistance acts as a drag force, reducing the velocity and maximum height of the arrows.

What is the relationship between kinetic and potential energy during the arrows’ motion?

At the highest point, kinetic energy is converted into potential energy, and vice versa during descent.